假设对于函数 f 有:
x→climf(x)=L
即:只要 x 无限接近于 c, 则 f(x) 必然无限接近于 L。
用 ε−δ 语言来描述就是:
∀ε>0, ∃δ>0, s.t. 0<∣x−c∣<δ⟹∣f(x)−L∣<ε说白了就是:无论给定任何一个数字 ε(ε>0),总能找到一个数 δ(δ>0)。使当 x 在 c 的 δ 范围内时,f(x) 在极限 L 的 ε 范围内。
例:已知 f(x)={2xxx=5x=5, 证明 x→5limf(x)=10
根据定义,给定任意 ε(ε>0),有 δ(δ>0)。因此,我们本质上是要找到一个 δ=function of ε 的函数。
Proof.
∣x−5∣<δ⟹∣2x−10∣<ε∣2x−10∣<2δ2δ=ε⇒δ=2ε∣2x−10∣<ε∀ε>0, ∃δ>0, s.t. ∣x−5∣<δ⟹∣2x−10∣<ε Q.E.D.
设 I 为包含某点 c 的区间,f,g,h 为定义在 I 上的函数。若对于所有属于 I 而不等于 c 的 x,有:
- g(x)⩽f(x)⩽h(x)
- x→climg(x)=x→climh(x)=L
则,x→climf(x)=L。
g(x) 和 h(x) 分别被称为 f(x) 的下界和上界。
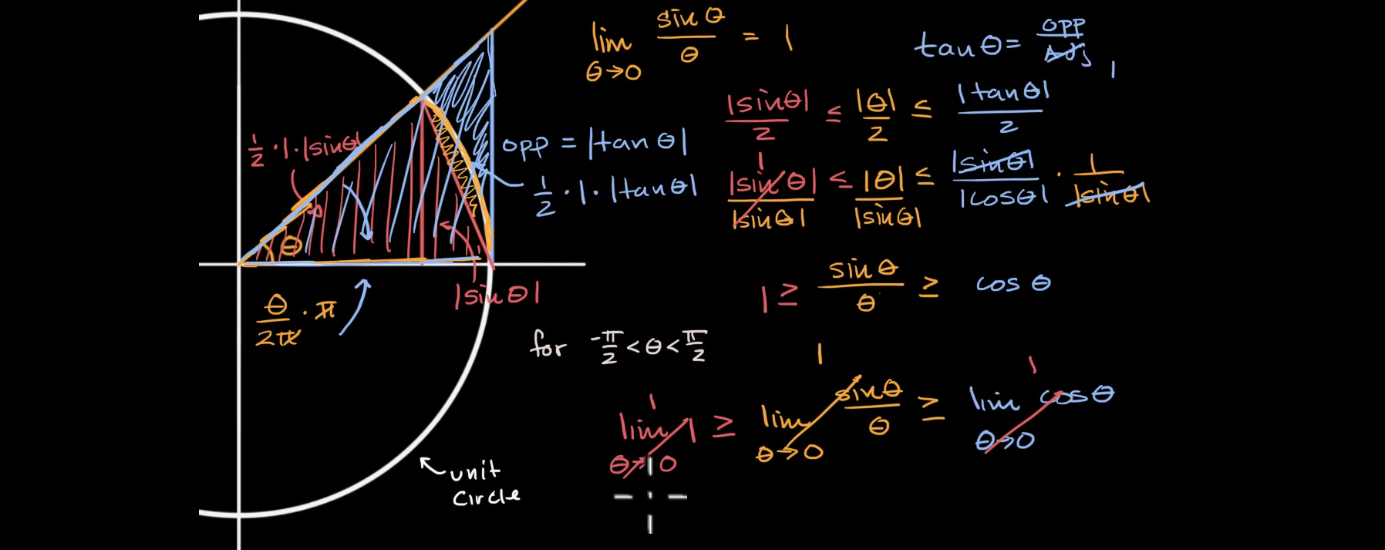
Proof.
θ→0limθ1−cosθ=θ→0limθ(1+cosθ)(1−cosθ)(1+cosθ)=θ→0limθ(1+cosθ)sin2θ=θ→0limθsinθ⋅θ→0lim1+cosθsinθ=1⋅0=0Q.E.D.函数在某一点处连续:f is continuous at x=c⟺x→climf(x)=f(c)
函数在开区间连续:f is continuous over (a, b)⟺f is continuous over every point in the interval
函数在闭区间连续:f is continuous over [a, b]⟺f is continuous over (a, b) and x→a+limf(x)=f(a), x→b−limf(x)=f(b)
Suppose f is a continuous function at every point of the interval [a, b]
- f will take on every value between f(a) and f(b) over the interval
- For any L between the values f(a) and f(b), there exists a number c in [a, b] for which f(c)=L
怎么会有这么简单的定理…
Lagrange's notation: f′
Leibniz's notation: dxdy
Newton's notation: y˙
f′(x)=h→0limhf(x+h)−f(x)
f′(c)=x→climx−cf(x)−f(c)
f is differentiability at x=c⟹f is continuous at x=cf is not continuous at x=c⟹f is not differentiability at x=c
不可微的三种情况:⎩⎨⎧1. not continuous2. vertical tanget3. sharp turn
Proof.
Assume: f differentiability at x=c
∵f differentiability at x=c∴f′(c)=x→climx−cf(x)−f(c)
x→clim[f(x)−f(c)]x→clim[f(x)−f(c)]x→climf(x)−x→climf(c)x→climf(x)−f(c)x→climf(x)=x→clim(x−c)⋅x−cf(x)−f(c)=x→clim(x−c)⋅x→climx−cf(x)−f(c)=0⋅f′(c)=0=0=0=0=f(c)Q.E.D.Proof.
dxd(xn)=Δx→0limΔx(x+Δx)n−xn
According to Binomial theorem:
Δx→0limΔx(x+Δx)n−xn=Δx→0limΔxxn+(1n)xn−1Δx+(2n)xn−2Δx2+...+(nn)x0Δxn−xn=Δx→0lim(1n)xn−1+(2n)xn−2Δx+...+(nn)Δxn−1=Δx→0lim(1n)xn−1=Δx→0lim1!(n−1)!n!xn−1=Δx→0limnxn−1Q.E.D.Proof.
dxd(x)=Δx→0limΔxx+Δx−x=Δx→0limΔx(x+Δx+x)(x+Δx−x)(x+Δx+x)=Δx→0limx+Δx+x1=Δx→0lim2x1=Δx→0lim21x−21Q.E.D.Proof.
∵k is constant∴y does not change as x changes∴f(x+h)−f(x)=0∴dxdk=h→0limhf(x+h)−f(x)=h→0limh0=0Proof: Constant multiple and sum/difference rules
Constant multiple rule: dxd[k⋅f(x)]=k⋅dxdf(x)
Sum rule: dxd[f(x)+g(x)]=dxdf(x)+dxdg(x)
Difference rule: dxd[f(x)−g(x)]=dxdf(x)−dxdg(x)
Proof.
1. f(x)=kg(x)⟹f′(x)=kg′(x)
f′(x)=h→0limhf(x+h)−f(x)=h→0limhkg(x+h)−kg(x)=h→0limk(hg(x+h)−g(x))=kh→0limhg(x+h)−g(x)=kg′(x)Q.E.D.2. f(x)=g(x)±j(x)⟹f′(x)=g′(x)±j′(x)
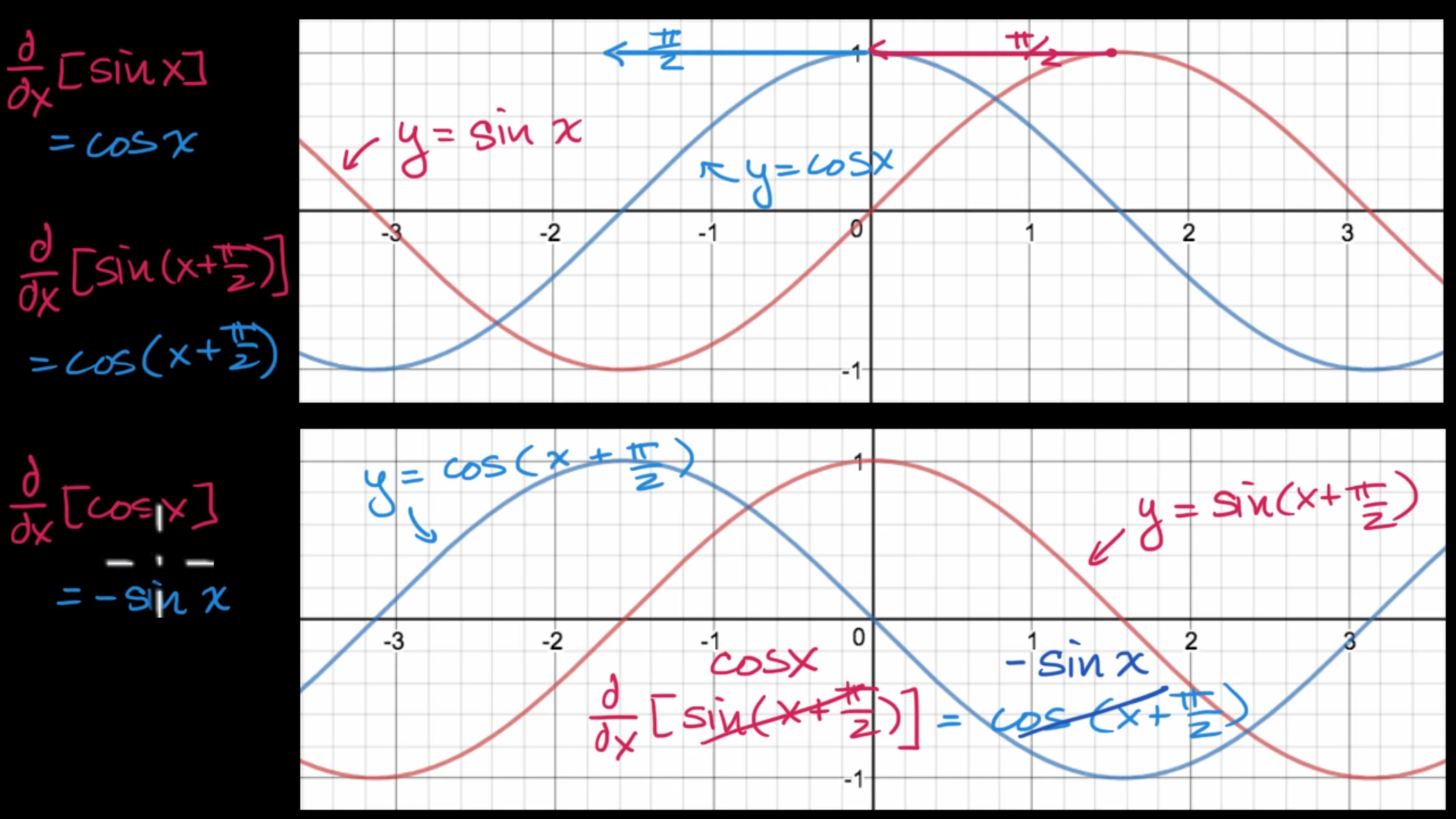
f′(x)=h→0limhg(x+h)±j(x+h)−(g(x)±j(x))=h→0lim(hg(x+h)−g(x)±hj(x+h)−j(x))=h→0limhg(x+h)−g(x)±h→0limhj(x+h)−j(x)=g′(x)±j′(x)Q.E.D.Proof: The derivatives of sin(x) and cos(x)
Known x→0limxsinx=1 and x→0limx1−cosx=0
Proof.
1. dxd[sinx]=cosx
dxd[sinx]=Δx→0limΔxsin(x+Δx)−sin(x)=Δx→0limΔxcosxsinΔx+sinxcosΔx−sinx=Δx→0lim(ΔxcosxsinΔx+ΔxsinxcosΔx−sinx)=Δx→0limcosx(ΔxsinΔx)+Δx→0limΔxsinx(cosΔx−1)=cosxΔx→0limΔxsinΔx−sinxΔx→0limΔx1−cosΔx=cosx⋅1−sinx⋅0=cosxQ.E.D.2. dxd[cosx]=−sinx
Know the limit definition of e is e=n→∞lim(1+n1)n=n→0lim(1+n)n1
Proof.
dxd(ex)=Δx→0limΔxex+Δx−ex=exΔx→0limΔxeΔx−1Let n=eΔx−1, we can get n+1=eΔx, such that Δx=ln(n+1) and as Δx→0=n→0
We can rewrite to:
dxd(ex)=exn→0limln(n+1)n=exn→0limn1ln(n+1)n1n=exn→0limln[(1+n)n1]1=exln[n→0lim(1+n)n1]1=exQ.E.D.Proof.
dxd(lnx)=Δx→0limΔxln(x+Δx)−ln(x)=Δx→0limΔxln(xx+Δx)=Δx→0limΔxln(1+xΔx)=Δx→0limΔx1ln(1+xΔx)=Δx→0limln[(1+xΔx)Δx1]Let n=xΔx, Δx=nx, Δx1=n1⋅x1 and as Δx→0=n→0
We can rewrite to:
Δx→0limln[(1+xΔx)Δx1]=x1n→0limln[(1+n)n1]=x1ln[n→0lim(1+n)n1]=x1Q.E.D.Method 2 (Using the fact that dxd(ex)=ex and applying implicit differentiation)
Proof.
Known dxd(ex)=ex
Let y=ln(x), we can get:
dxd(ey)ey⋅dxdydxdy=dxd(x)=1=ey1=elnx1=x1Q.E.D.Proof.
dxd[f(x)g(x)]=h→0limhf(x+h)g(x+h)−f(x+h)g(x)+f(x+h)g(x)−f(x)g(x)=h→0lim[f(x+h)hg(x+h)−g(x)+g(x)hf(x+h)−f(x)]=[h→0limf(x+h)][h→0limhg(x+h)−g(x)]+[h→0limg(x)][h→0limhf(x+h)−f(x)]=f(x)g′(x)+g(x)f′(x)Q.E.D.Proof: The derivatives of tan(x)、cos(x)、sec(x) and csc(x)
Proof.
dxd(tanx)dxd(secx)=dxd(cosxsinx)=cos2xcos2x+sin2x=cos2x1=sec2x=dxd(cosx1)=cos2x0⋅cosx+1⋅sinx=cos2xsinx=tanx⋅secxdxd(cotx)dxd(cscx)=dxd(sinxcosx)=sin2x−(sin2x+cos2x)=−sin2x1=−csc2x=dxd(sinx1)=sin2x0⋅sinx−1⋅cosx=−sin2xcosx=−cotx⋅cscxQ.E.D.Proof.
Known dxd(ex)=ex
Let a=elna
dxd(ax)=dxd[(elna)x]=dxd[e(lna)x]=e(lna)x⋅lna=ax⋅lnaQ.E.D.Proof.
Known dxd(lnx)=x1
dxd(logax)=dxd(lna1⋅lnx)=xlna1Q.E.D.Proof: Chain Rule and Quotient Rule
Chain Rule Proof.
Known: 1. If a function is differentiable, then it is also continuous.2. If function u is continuous at x, then Δu→0 as Δx→0For why if function u is continuous at x, then Δu→0 as Δx→0:
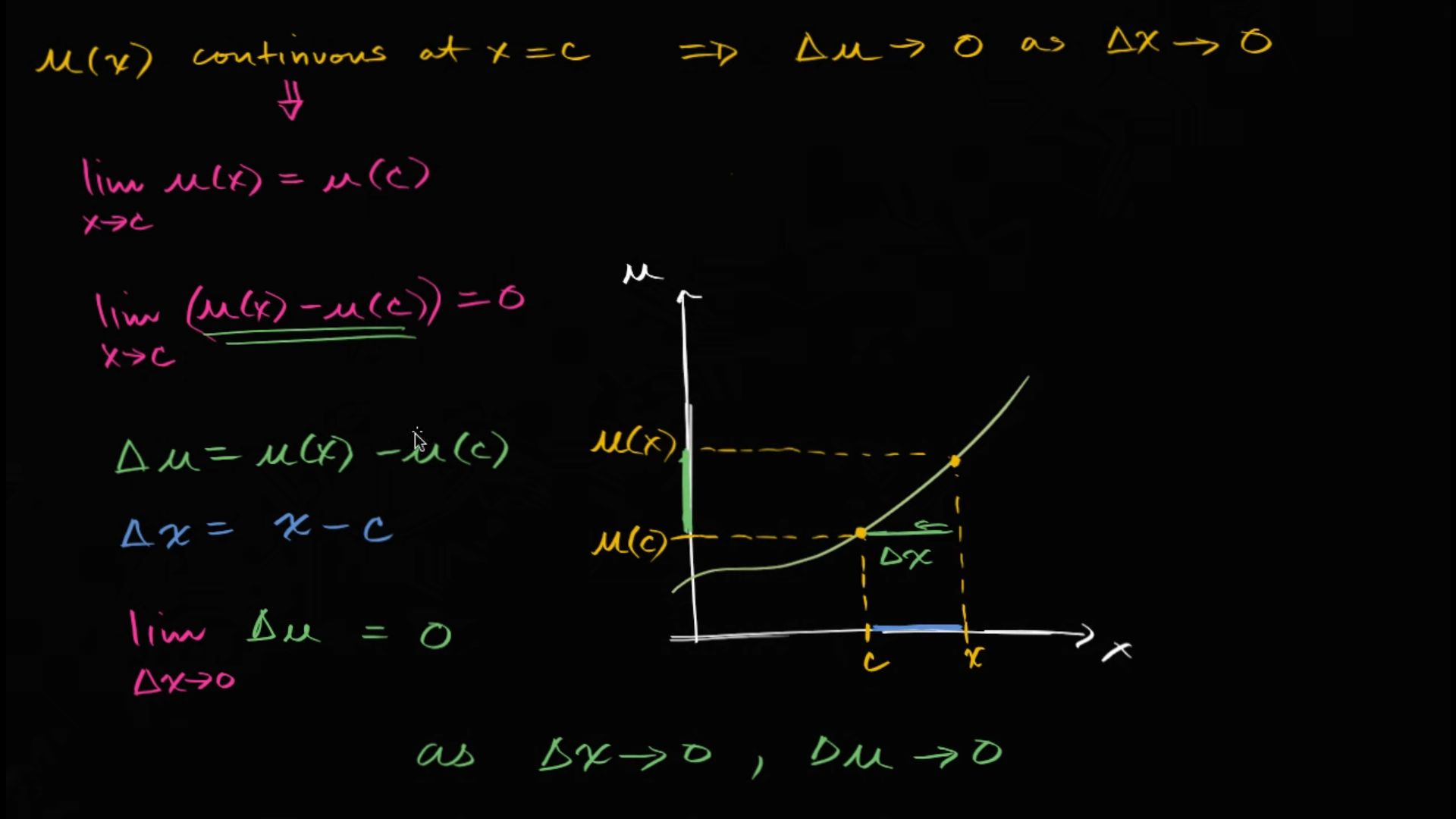
The chain rule tell us: dxd[y(u(x))]=dxdy=dudy⋅dxdu
Assuming y, u differentiable at x. We can get:
dxdy=Δx→0limΔxΔy=Δx→0limΔuΔy⋅ΔxΔu=(Δx→0limΔuΔy)(Δx→0limΔxΔu)=(Δu→0limΔuΔy)(Δx→0limΔxΔu)=dudy⋅dxduQ.E.D.Quotient Rule Proof.
dxd[g(x)f(x)]=dxd[f(x)⋅[g(x)]−1]=f′(x)[g(x)]−1−f(x)[g(x)]−2g′(x)=g(x)f′(x)−[g(x)]2f(x)g′(x)=[g(x)]2f′(x)g(x)−f(x)g′(x)Q.E.D.NOTE
This isn't full proof of L'Hôpital's rule, just a special case. But it should give some intuition for why it works.



